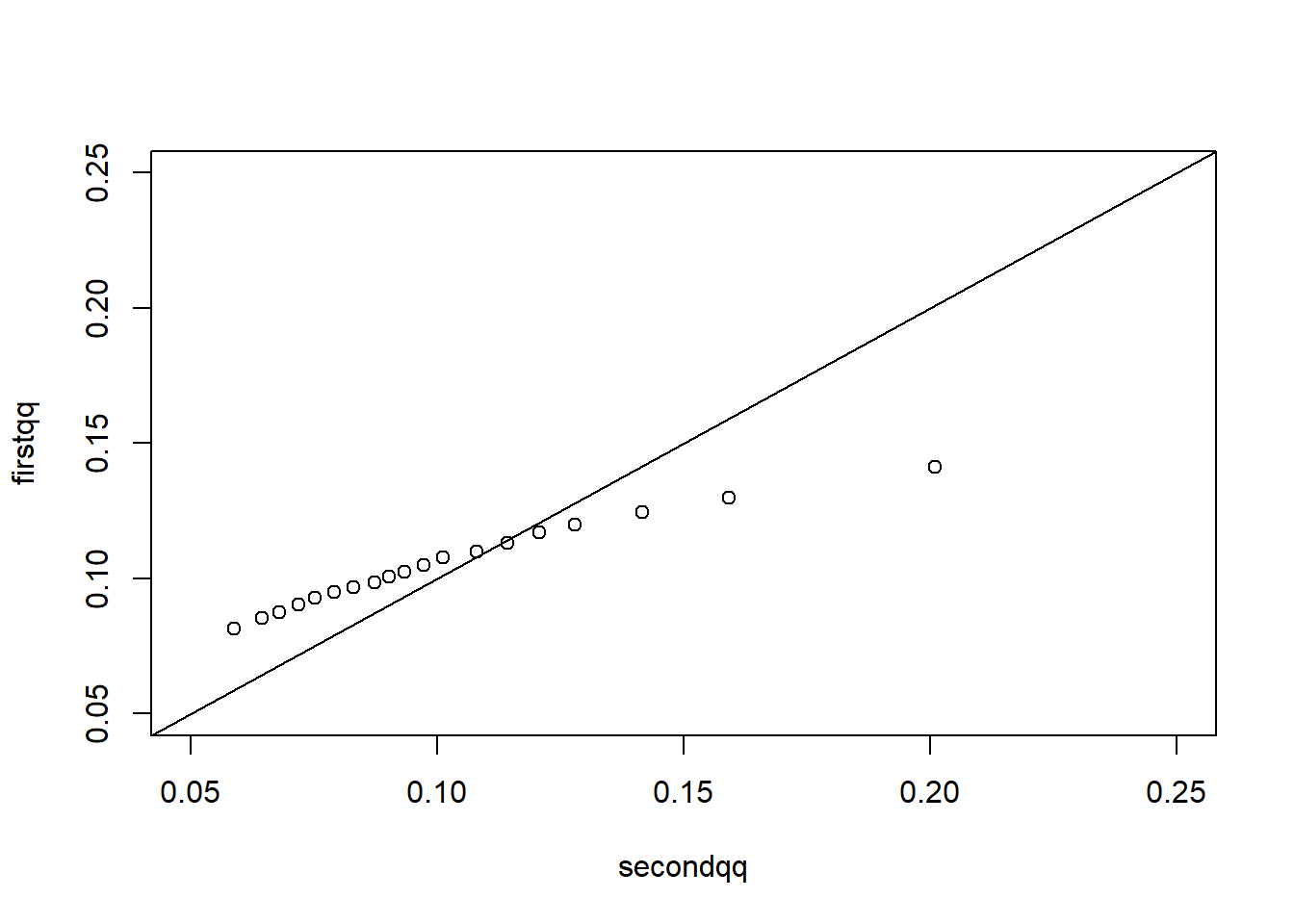
I am reading (Efron and Hastie 2016) and try to reproduce the graph (Hinkley, David and Efron, Bradley 1977), this kind of confuse me, just make a note to update.
cauchy.mle <- function(x,start,eps=1.e-8,max.iter=50){
if (missing(start)) start <- median(x)
theta <- start
n <- length(x)
score <- sum(2*(x-theta)/(1+(x-theta)^2))
iter <- 1
conv <- T
while (abs(score)>eps && iter<=max.iter){
info <- sum((2-2*(x-theta)^2)/(1+(x-theta)^2)^2)
theta <- theta + score/info
iter <- iter + 1
score <- sum(2*(x-theta)/(1+(x-theta)^2))
score2<-sum((2*(x-theta)/(1+(x-theta)^2))^2)
}
if (abs(score)>eps) {
print("No Convergence")
conv <- F
}
loglik <- -sum(log(1+(x-theta)^2))
info <- sum((2-2*(x-theta)^2)/(1+(x-theta)^2)^2)
r <- list(theta=theta,loglik=loglik,score=score,score2=score2,info=info,convergence=conv)
r
}
first <- NULL
second <- NULL
mle<-c()
for(i in 1: 1000){
x<- rcauchy(20)
r2 <- cauchy.mle(x,start=median(x),max.iter=100)
mle<-c(mle,r2$theta)
first <- c(first,1/r2$score2)
second<-c(second,1/r2$info)
}
firstqq<-quantile(first, probs=seq(0.05,1, by=0.05))
secondqq<-quantile(second, probs=seq(0.05,1, by=0.05))
re<-data.frame(mle,first,second)
var(mle[which(second<secondqq[1])])
#second
#theta=20
#3integrate(function(x){(2*(x-theta)/(1+(x-theta)^2))^2*dcauchy(x,theta,1)},lower=-Inf, upper=Inf ,abs.tol=1.e-8)$value*20
##mlevar<-first^2*d
qqplot(secondqq,firstqq,xlim=c(0.05,0.25),ylim=c(0.05,0.25))
abline(0,1)